Dynamisk posisjonering (DynPos eller DP)

Dynamisk posisjonering = posisjonering av fartøyer vha. posisjonsregulering der trustere styres for å holde fartøyet i riktig posisjon i forhold til f.eks. havbunnen eller en plattform eller et annet fartøy.

Hva semesteroppgaven går ut på

I denne oppgaven skal dere designe og simulere et system for dynamisk posisjonering i LabVIEW. Systemet inkluderer et Kalmanfilter for estimering av omgivelseskraft på fartøyet. (Dette estimatet benyttes i regulatorfunksjonen.)

Utstyr og programvare

PC med LabVIEW
Simulatoren dynpos.vi for posisjonsregulering for fartøyet beskrevet nedenfor. Simulatoren inneholder ikke Kalmanfilter. Det skal dere selv implementere, gjerne med utgangspunkt i forannevnte VI.

Oppgaver

Først litt bakgrunnsinformasjon: Figur 1 viser hovedkomponentene i et DP-system.

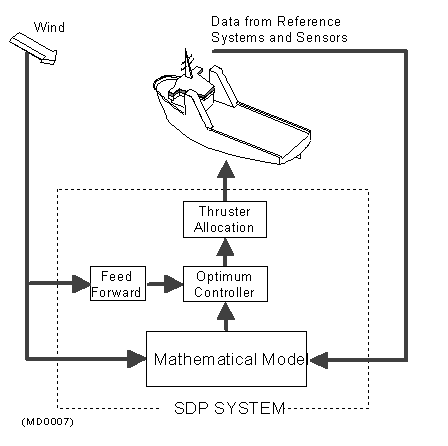
Figur 1. (Kilde: Kongsberg Maritime)

Figur2 viser et fartøy med definisjon av de båtfaste koordinatretningene surge, sway og yaw (det er vanlig å bruke engelske betegnelser også i norsk fagspråk).

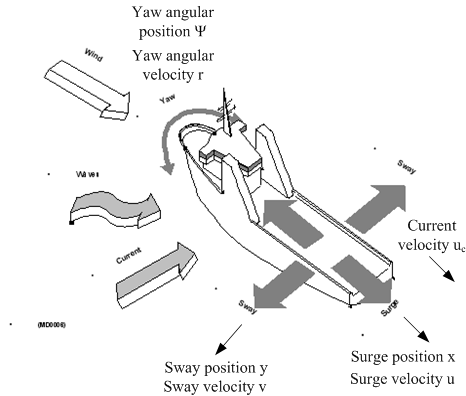
Figur 2. (Kilde: Kongsberg Maritime)

Figur 3 viser sammenhengen mellom et jordfast koordinatsystem og et båtfast koordinatsystem.

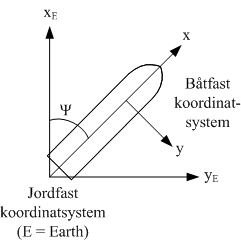
Figur 3

Nedenfor er vist en forenklet matematisk modell av fartøyet. Modellen uttrykker kraftbalansene i surge-retningen og i sway-retningen og samt momentbalansen i yaw-retningen (rotasjonen).

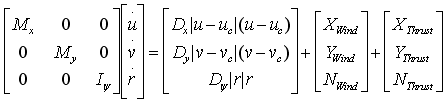
X og Y betyr kraft, og N betyr moment. Subindeks c betyr strøm (engelsk: current). M er masse, og I er treghetsmoment. D er dempekoeffisient. Leddet D_x|u-u_c|(u-u_c) representerer en hydrodynamisk kraft, F_x.

Til orientering: Nedenfor er vist koodinattransformasjonen av hastigheter i det båtfaste koordinatsystemet til hastigheter i det jordfaste koordinatsystemet. (Denne transformasjonen trengs imidlertid ikke i oppgavene nedenfor.)

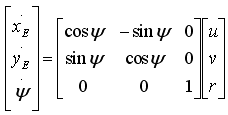
I oppgavene nedenfor skal dere for enkelhets skyld betrakte fartøyets bevegelse i kun i surge-retningen. Det er ikke bevegelse i noen andre retninger.

Anta følgende (gjelder for et bestemt testfartøy):

M_x = 71164 tonn
D_x = -8.4 kN/(m/s*m/s)
Langskips vindkraft er gitt ved
X_Wind = V_w²[c_Wx1 cos(fi) + c_Wx2cos(3fi)]

der V_w er vindhastighet relativ båten. fi er båt-relativ vindretning. Dersom vinden kommer rett forfra båten, er fi = 180 grader. c_Wx1 = 0,1838 og c_Wx2 = -0,0068 er såkalte 1. og 2. ordens vindkoeffisienter. Eksempel: Med V_w = 20 m/s og fi=180 grader, blir X_Wind = -70,8 kN.
u_c varierer typisk i området 0 - 3 m/s. (u_c skal estimeres med Kalmanfilter.)
Langskips thrusterkraft X_Thrust (pådraget på fartøyet) har en begrensning på 552 kN forover og 467 kN bakover.
Til info (trengs egentlig ikke i oppgaven): Fartøyets lengde er L_pp = 233 meter. Bredden er 42 meter. Dypgang er 10 meter.

Kommentar: Innen DP-bransjen sier man "tonn" for en kraft på 1kN, men i denne oppgaveteksten representerer tonn ikke en kraft, men 1000kg, som normalt.

Skriv modellen for fartøyets bevegelse i surge-retningen på tilstandsromform. (Tips: Innfør x₁ = posisjon og x₂ = hastighet. Utgangsvariabelen er x₁.) Er modellen lineær eller ulineær?
Implementer en simulator med følgende innhold:
- Fartøymodellen (fra deloppgave 1). Vindhastigheten og vannstrømhastigheten skal være justerbare fra frontpanelet.
- Et Kalmanfilter basert på følgende:
  - Kun posisjonen x₁ måles.
  - u_c antas å være konstant, og den skal estimeres. Denne konstantens antatte kovarians kan være Kalmanfilterets tuningsfaktor.
  - I Kalmanfilteret i simulatoren skal den stasjonære Kalmanfilterforsterkningen, K_s, benyttes. K_s skal beregnes fra en fast, lineær fartøymodell basert på linearisering omkring "nullarbeidspunktet" der alle variable har verdi lik null. K_s skal beregnes vha. funksjonen CD Kalman Gain (på Control Design-funksjonspaletten). Denne beregningen kan foregå én gang for alle (utenfor Simulation Loop).
    Tips mhp. Kalmanfilteret: Det viser seg at systemet er såkalt ikke-observerbart i nullarbeidspunktet, hvilket betyr at det ikke er garantert at Kalmanfilteret konvergerer mot korrekte estimater, og det vil da heller ikke eksiterere noen stasjonær Kalmanfilterforsterkning. Dette problemet kan omgås ved å modifisere litt på modellen slik at systemet allikevel blir observerbart i nullarbeidspunktet. En slik modifikasjon er å sørge for at element A(1,2) i den tidskontinuerlige systemmatrisen i den lineære modellen er forskjellig fra null. Dere kan prøve f.eks. verdien 1e-8.
  - Kalmanfilterlikningene bør skrives i en Formula Node i LabVIEW.
- Et posisjonsreguleringssystem for fartøyet basert på ulineær dekopling med "intern" PID-regulator. Dere kan imidlertid droppe foroverkoplingen fra akselerasjonsreferansen dr²/dt². I regulatoren må estimater fra Kalmanfilter benyttes der målinger ikke fins (kraften F_x beregnes fra Kalmanfilterestimatene av u og u_c, jf. fartøymodellen gjengitt ovenfor). PID-parametrene kan stilles inn ihht. Skogestads metode slik at reguleringssystemet får en responstid på ca. 1min. Skogestads metode for prosesser uten tidsforsinkelse er vist i tabellen nedenfor (fra PID Control).
Uttesting av DP-systemet:
1. Virker Kalmanfilteret tilfredsstillende?
2. Anta at posisjonsreferansen endres som et sprang (fra 0). Virker posisjoneringssystemet tilfredsstillende? Prøv også andre typer referansesignal enn sprang. Prøv også med varierende vindhastighet og varierende vannstrøm.
3. I regulatorfunksjonen inngår estimat av kraften F_x. Er det fordelaktig å ha dette leddet i regulatoren?

Framdriftsplanen

Oppdatert 5.3.05 av Finn Haugen. E-post: finn@techteach.no.